기계학습_나이브 베이지안 분류기(Naive Bayesian classifier)

데이터 정제, 전처리

: 훈련데이터에 에러, 이상치(outlier) 등이 있으면 기계학습 시스템이 내재된 패턴을 찾기 힘들기 때문에 적절한 작업이 필요

일부 샘플에 특성 몇 개가 빠져있으면, 이 특성을 무시할 지, 이 샘플을 무시할 지, 빠진 값을 (평균값 등으로) 채워 넣을지를 결정. 경우에 따라서는 이들을 제거한 모델과 적절하게 채워넣은 모델을 각각 훈련시켜 비교

isnull() 메소드: 빠진 샘플 확인

fillna() 메소드: 빠진 샘플 채우기 ; inplace=True 바로 변수 대체

dropna() 메소드: 빠진 샘플 삭제

일부 샘플이 이상치라는 것이 명확하면 제거, 그렇지 않으면 수정 (데이터에 대한 사전 지식이 필요)
표본에 대한 다양한 통계량(표본의 몇 몇 특성을 수치화한 것)을 이용하여 판단:

표본평균, 표본분산, 최솟값, 최댓값, 중앙값, 표본 분위수(quantile) 등

Pandas의 분위수 API
- boxplot
Pandas의 DataFrame에 대한 plot.box() API

Pandas의 DataFrame에 대한 boxplot() API : 더 많은 파라미터를 가지고 있다.

데이터 실습 with PimaIndiansDiabetes.csv

PimaIndiansDiabetes.csv: Pima Indian(미국 토착 인디언 부족) 768명의 성인 여성의 의료 정보와 당뇨병 여부가 담긴 데이터셋

-출처: kaggle

데이터 정제

data = pd.read_csv('./datasets/PimaIndiansDiabetes.csv') #csv 데이터 읽기
data_subset = data.loc[:,['Blood Glucose', 'BMI', 'Class']] #혈당, BMI, 당뇨병 여부(1,0) 데이터만 추출

data_subset.quantile([0.25,0.5,0.75])
data_subset[['Blood Glucose', 'BMI']].plot.box() # quantile값, 상자그림을 통해 이상치 파악 및 데이터 탐색

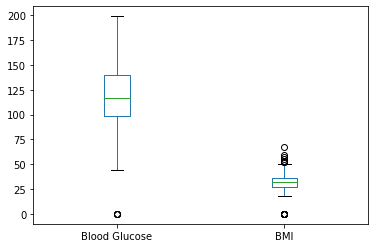
plotbox

혈당과 BMI 모두 0 근처에서 이상치 발견» 최솟값을 이용해 값 확인

print(data_subset.min()) #모두 최솟값이 0으로 나옴

두 변수 모두 당뇨병 진단과 관련성이 있으므로 하나라도 0이면 샘플 삭제, 두 변수 모두 0의 값을 가질 수는 없다.

bg_mask = data_subset.loc[:,"Blood Glucose"]!=0
bmi_mask = data_subset.loc[:,"BMI"]!=0
clean_data_subset = data_subset[bg_mask & bmi_mask]

X_train0,X_train1의 각 열에 대해 히스토그램을 그려 p(x1 0),p(x1 1),p(x2 0),p(x2 1)을 추정

X = clean_data_subset.loc[:, ['Blood Glucose', 'BMI']] # 특성벡터 지정
y = clean_data_subset.loc[:, 'Class'] #레이블 지정

from sklearn.model_selection import train_test_split 
X_train, X_test, y_train, y_test = train_test_split(X,y, random_state=20) #데이터셋 훈련용과 테스트용으로 나누기

X_train0 = X_train[y_train==0] 
X_train1 = X_train[y_train==1]
m0 = (y_train==0).sum()
m1 = (y_train==1).sum() #class별 갯수

plt.hist(X_train0.loc[:,'Blood Glucose'],bins='fd',density=True)
X_train0.loc[:,'Blood Glucose'].plot.density() #p(x1|0)

plt.hist(X_train0.loc[:,'BMI'],bins='fd',density=True)
X_train0.loc[:,'BMI'].plot.density()   #p(x2|0)

plt.hist(X_train1.loc[:,'Blood Glucose'],bins='fd',density=True)
X_train1.loc[:,'Blood Glucose'].plot.density()  #p(x1|1)

plt.hist(X_train1.loc[:,'BMI'],bins='fd',density=True)
X_train1.loc[:,'BMI'].plot.density() #p(x2|1)

# bins='fd' 는 Freeman-Diaconis rule에 의해 가장 분포를 잘 보여주는 bin의 갯수를 결정한다. 
# X 변수와 y 레이블에 따라 분포가 히스토그램이 어떻게 그려지는지 파악한다. 

위 히스토그램을 보고 완벽하게 같진 않지만 정규분포라고 가정하고 확률함수를 계산해보자

def fit_distribution(data, col_idx):
    #정규분포의 평균과 표준편차를 추정 S
    mu = data[:,col_idx].mean()
    sigma = data[:,col_idx].std(ddof=0) #pd.Series.std(ddof=0)은 표준편차/ 
    								 #pd.Series.std(ddof=1)은 표본표준편차(default)    
    
    # 확률분포 구하기 
    dist = norm(mu, sigma)
    return dist

X_train0 = X_train0.to_numpy() #훈련데이터를 Numpy array로 바꾼다. 
X_train1 = X_train1.to_numpy()

distX1y0 = fit_distribution(X_train0, 0) #'Blood Glucose'
distX2y0 = fit_distribution(X_train0, 1) #'BMI'
distX1y1 = fit_distribution(X_train1, 0) #'Blood Glucose'
distX2y1 = fit_distribution(X_train1, 1) #'BMI'

prior0 = m0/(m0+m1)
prior1 = m1/(m0+m1) #사전확률

print(f"P(y=1)={prior1:.3f}, P(y=0)={prior0:.3f}") #P(y=1)=0.361, P(y=0)=0.639

#p(x,0)=p(0)p(x1|0)p(x2|0) 와  p(x,1)=p(1)p(x1|1)p(x2|1) 을 계산
def joint_prob(data, prior, distX0, distX1):
    return prior * distX0.pdf(data[:,0]) * distX1.pdf(data[:,1]) 

# 훈련 데이터셋에 대한 예측 
train_prob0 = joint_prob(X_train.to_numpy(), prior0, distX1y0,distX2y0)
train_prob1 = joint_prob(X_train.to_numpy(), prior1, distX1y1,distX2y1)

train_prediction = (train_prob1>train_prob0).astype(int)

# 정확도 계산
train_acc = (train_prediction == y_train).sum()/len(y_train)

print(f"훈련 데이터셋에 대한 정확도={train_acc * 100 : .1f}%")
#테스트 데이터셋에 대한 정확도= 77.5%

# 테스트 데이터셋에 대한 예측 
test_prob0 = joint_prob(X_test.to_numpy(), prior0, distX1y0,distX2y0)
test_prob1 = joint_prob(X_test.to_numpy(), prior1, distX1y1,distX2y1)

test_prediction = (test_prob1>test_prob0).astype(int)

# 정확도 계산
test_acc = (test_prediction == y_test).sum()/len(y_test)

print(f"테스트 데이터셋에 대한 정확도={test_acc * 100 : .1f}%")

#테스트 데이터셋에 대한 정확도= 77.5%

Scikit-learn의 나이브 베이즈 분류기 사용하기

sklearn.naive_bayes module의 GaussianNB가 $p(X|y)$ 를 정규분포로 가정하는 나이브 베이즈 분류기

from sklearn.naive_bayes import GaussianNB #GaussianNB 분류기 불러오기

classifierGNB = GaussianNB()
classifierGNB.fit(X_train, y_train) #훈련

train_acc = classifierGNB.score(X_train,y_train) #훈련셋의 정확도
test_acc = classifierGNB.score(X_test,y_test) #테스트셋의 정확도

print(f"Prediction Accuracy for Train Data set:{train_acc :.3f}\nPrediction Accuracy for Test Data set:{test_acc :.3f}")
#Prediction Accuracy for Train Data set:0.757
#Prediction Accuracy for Test Data set:0.775

classifierGNB.predict_proba(X_test)[:5]
#array([[0.5866136 , 0.4133864 ],[0.32890518, 0.67109482],[0.55879185, 0.44120815],[0.93848913, 0.06151087],[0.89546209, 0.10453791]])

분류문제에 대한 학습모델의 성능 평가 기준

학습모델 성능평가 기준으로 정확도를 이용했지만 경우에 따라 다른 기준이 의미를 가진다.

예) 임상자료를 이용하여 환자가 특정 희귀 암에 걸렸는지(양성: 레이블1 ,음성: 레이블2)를 분류하는 학습 모델의 경우 정확도는 좋은 모델의 측도로 적합하지 않음

100명 중 한 명이 암에 걸린 경우, 모든 환자가 음성이라고 판별하는 학습모델의 경우 정확도는 99%지만 쓸모없는 학습모델임
분류기의 성능을 평가하는 좋은 방법은 오차행렬(Confusion matrix) 또한 이를 요약한 지표를 살펴보는 것이다.

Reference:

기계학습_하길찬 교수님 수업을 바탕으로 공부한 내용입니다.
귀퉁이 서재님의 나이브 베이즈 분류
Generative model과 Discriminate model, BLOG_용이

← Previous Post Next Post →