기계학습_선형회귀 모델, 경사 하강법

선형 모델

회귀 문제에서 특성벡터 $x = (x_1,\cdots,x_n)^{\rm T}$의 특성값 $x_i\, (i=1,\cdots,n)$에 대한 선형결합으로 레이블 $y$ 를 예측하는 학습 모델
분류문제에 대한 판별경계를 특성값에 대한 선형결합을 이용하여 결정하는 학습모델

선형회귀 학습모델

지도학습
훈련 데이터셋 아래에 대한 학습모델을 다음과 같이 각 특성값에 대해 선형이 되도록 가정하는 판별모델의 일종

\[\{(\mathbf x_i,\mathbf y_i)|1\le i\le m\} (단,\mathbf x_i=(x_{i1},\cdots,x_{in})^{\rm T})\] \[\hat y = \theta_0 +\theta_1 x_1+\cdots +\theta_nx_n\]

편향(또는 절편) $\theta_0$와 가중치 $\theta_i\, (1\le i\le n)$를 합쳐서 모델 파라미터
$n$차원 특성벡터 $x=(x_1,\cdots,x_n)^{\rm T}$를 $\mathbf x=(1,x_1,\cdots,x_n)^{\rm T}$로 쓰고(즉, $x_0=1$), ${\theta} = (\theta_0,\theta_1,\cdots,\theta_n)^{\rm T}$로 나타내면 위 모델은 $\hat y = h_{{\theta}}(\mathbf x)=\theta^{\rm T}\mathbf x$로 간단히 나타낼 수 있음
n=1일 때를 단순선형회귀 모델, $n>1$일 때를 다중선형회귀 모델이라고 함

이 모델을 학습시킨다는 것은 모델이 훈련 데이터셋에 가장 잘 맞도록 모델 파라미터 $\theta$를 설정하는 것.

실제로는 평균제곱오차 (MSE)가 최소가 되는 $\theta$ 를 설정

\[\text{MSE}({\theta})=\bigl(\text{ 또는 손실함수 }L({\theta})\bigr) = \dfrac 1 m \sum_{i=1}^m(\hat y_i -y_i)^2 =\dfrac 1 m (\hat{\mathbf y}-\mathbf y)^{\rm T} (\hat{\mathbf y}-{\mathbf y})=\dfrac 1 m (\mathbf X{\theta}-\mathbf y)^{\rm T}(\mathbf X{\theta}-\mathbf y) \cdots \cdots (1)\]
MSE가 최소가 되는 $\boldsymbol{\theta}$를 구하는 것은 RSS(Residual Sum of Square)$=\sum_{i=1}^m (\hat y_i - y_i)^2$이 최소가 되는 $\boldsymbol{\theta}$를 구하는 것과 같음
MSE는 일종의 비용함수

선형회귀 모델의 학습(해석적 방법)

식 (1)에서 손실함수 $L(\boldsymbol{\theta})$는 모델 파라미터 $\theta_0,\cdots,\theta_n$에 대해 이차식이므로 $\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})=\mathbf 0$를 만족하는 $\boldsymbol{\theta}=\hat{\boldsymbol{\theta}}$에서 최소가 된다.
그래디언트를 열벡터: $\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta}) = \left(\dfrac{\partial L}{\partial \theta_0}(\boldsymbol{\theta}),\cdots,\dfrac{\partial L}{\partial \theta_n}(\boldsymbol{\theta})\right)^{\rm T}$

\[(\nabla_ L({\theta})) = \dfrac 2 m \mathbf X^{\rm T}(\mathbf X{\theta}-\mathbf y)=\mathbf 0 \cdots \cdots (2)\]

이 성립하는 $\hat{\theta}$를 구하면 $\hat = (\mathbf X^{\rm T}\mathbf X)^{-1}\mathbf X^{\rm T}\mathbf y$

선형회귀 모델의 학습(수치해석적 방법)

경사하강법:

경사 하강법의 기본 아이디어는 비용함수를 최소화하기 위해 반복해서 파라미터를 조정해가는 것 (구현 방법에 따라 배치 경사 하강법, 확률적 경사 하강법, 미니배치 경사 하강법 등이 있음)

\[{\theta}^{(t+1)}:= {\theta}^{(t)}-\alpha \nabla_L({\theta}^{(t)})\ (t\ge 0) \ \cdots \cdots (3)\]

모델의 극소값이 많을 때 올바른 최소값을 찾기 위해서 필요한 하이퍼 파라미터는 학습률 (learning rate) $\alpha$
학습률이 너무 작으면 수렴하는데 시간이 오래 걸리고, 너무 커도 시간이 오래 걸리거나 경우에 따라 수렴하지 않을 수도 있음 (아래 그림에서는 왼쪽의 학습률보다 오른쪽의 학습률이 큰 경우)

학습률

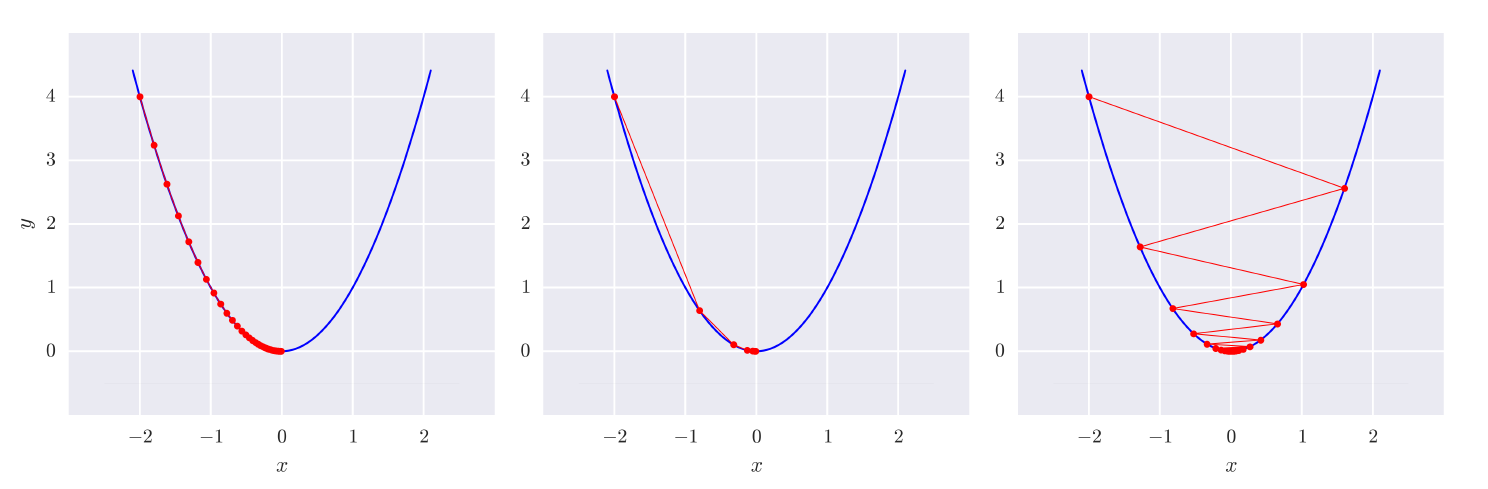
경사 하강법을 사용할 때는 반드시 모든 특성이 같은 스케일을 갖도록 만들어야함 - 수렴하는 시간의 단축을 위해
특성 스케일링(feature scaling) or 정규화(normalization)

min-max 스케일링: 모든 특성값이 0과 1 사이가 되도록 최소값을 뺀 후 최대값과 최소값의 차로 나눔

sklearn.preprocessing 모듈의 MinMaxScaler 변환기를 이용할 수 있음 (API)

표준화(standardization): 샘플의 각 속성별로 평균을 빼고 표준편차로 나눈다- 분산이 1이 되도록 조정

표준화 방법은 범위의 상한과 하한이 없어서 0과 1 사이 입력값을 기대하는 심층신경망에서는 문제가 될 수 있음.

sklearn.preprocessing 모듈의 StandardScaler 변환기를 이용할 수 있음 (API)

min-max 스케일링은 이상치에 영향을 많이 받지만 표준화는 이상치에 영향을 덜 받는다.
모든 스케일링 변환기에서 스케일링은 테스트 데이터셋을 제외한 훈련 데이터셋에 대해서만 fit() 메소드를 적용해야 함

경사 하강법의 구현

에포크(epoch): 경사 하강법에서 그래디언트를 업데이트시킬 때 , 훈련 데이터셋을 모두 사용하여 업데이트시키는 반복 단위

배치 경사 하강법(Batch Gradient Descent)

경사 하강법의 (3)을 반복적으로 계산할 때, 손실함수에 대한 그래디언트 벡터를 식 (2)와 같이 훈련 데이터셋 전체에 대해 계산하는 알고리즘 / 데이터셋 전체에 대해 기울기를 구해가는 경사 하강법
- 매우 큰 훈련 데이터셋에서는 느림
- 특성 수에는 민감하지 않으므로 선형회귀를 학습시킬 때, 역행렬을 구하거나 특이값 분해(SVD)를 이용하여 학습시키는 것보다 훨씬 빠름
적절한 학습률을 결정하는 방법:
- 그리드 탐색법을 이용하여 탐색
- 그리드 탐색에서 수렴하는데 시간이 너무 오래 걸리는 것을 방지하기 위해 반복 횟수를 제한
  - 반복 횟수를 제한하는 효율적인 방법은 반복 횟수를 아주 크게 지정하고, 그레디언트 벡터의 노름이 어떤 값 (허용오차 tolerance)보다 작아지면 알고리즘을 중지하는 방법

확률적 경사 하강법(SGD: Stochastic Gradient Descent)

확률적 경사 하강법은 배치 경사 하강법과 달리 (3)을 계산하는 매 단계에서 한 개의 샘플을 무작위로 선택하고 그 하나의 샘플에 대해 그레디언트를 업데이트(이 경우 식 (2)의 그래디언트 식에서 m=1)
(랜덤으로 한 곳을 선택하고 기울기를 구해서 작은 곳으로 가는 경사 하강법)

비용함수가 최솟값에 도달할 때까지 부드럽게 감소하지 않고 요동치지면서 평균적으로 최솟값에 근접

평균적으로 파라미터가 최솟값을 향해 진행하는 것을 보장하려면 파라미터를 업데이트할 때 사용하는 훈련 샘플이 독립동일분포(i.i.d)를 만족해야 함

위 조건을 만족하도록 구현하기 위해 한 에포크에서 훈련 데이터셋을 랜덤하게 섞은 후 하나씩 차례로 업데이트에 사용하고, 다음 에포크에서 다시 섞는 식의 방법을 사용할 수 있음

확률적 경사 하강법의 장점:
- 배치 경사 하강법은 매 스텝에서 전체 훈련 데이터셋을 사용하므로 훈련 데이터셋이 커지면 매우 느리지만, 확률적 경사 하강법은 매 반복에서 하나의 샘플만 메모리에 있으면 되므로 매우 빠르고 매우 큰 훈련 데이터셋에 대해서도 학습이 가능함
- 비용함수가 여러 개의 극솟값을 갖는 경우, 요동치며 특성으로 인해 극솟값을 건너 뛰는데 도움을 주어 배치 경사 하강법보다 최솟값에 근접할 가능성이 높음 »적절한 학습률 설정할 필요있다.
확률적 경사 하강법의 단점:
- 반면에 확률적이므로 이 알고리즘은 배치 경사 하강법에 비해 훨씬 불안정함
- 최적치에 근접한 값에 대응되는 좋은 파라미터를 구할 순 있지만, 최적치는 아님
무작위성이 갖는 장점과 단점의 딜레마를 해결하기 위해서 학습률을 점진적으로 감소시키는 방법을 적용
- 시작할 때는 학습률을 크게 하여 극솟값에 빠지지 않게 하고, 점차 줄여서 최솟값에 도달하도록 도와줌
- 학습률을 결정하는 함수를
  
  학습 스케쥴(learning schedule)
  
  예를 들어, 학습 스케쥴 함수 f를 f(t)=t0t+t1으로 잡을 수 있음 (단, t0,t1은 학습 스케쥴 함수에 대한 하이퍼파라미터)
sklearn.linear_model 모듈의 SGDRegressor에 확률적 경사 하강법이 구현되어 있음 (API)
- SGD 방식으로 선형회귀를 사용하려면 SGDRegressor의 입력 파라미터 중 loss=’squared_loss'(디폴트 값)을 이용하여 객체를 생성
- fit() 메소드의 입력으로 전달되는 y는 rank가 1인 넘파이 배열이어야 함
- 그 외 중요한 입력 파라미터와 디폴트 값:
  - max_iter=1000는 에포크 횟수
  - tol=1e-3는 한 에포크에서 0.001보다 적게 손실이 줄어들면 종료
  - eta0=0.01는 학습률 (SGDRegressor에서 alpha는 뒤에 배울 규제(regularization)와 관련된 파라미터)
  - penalty=l2는 규제의 종류 (규제없이 선형회귀를 할 때는 penalty=None으로 설정)
  - learning_ratestring='invscaling'는 학습 스케쥴 함수의 종류 (API 설명 참고)
  - early_stopping=False와 validation_fraction=0.1도 API 설명 확인

미니배치 경사 하강법(Mini-batch Gradient Descent)

매 업데이트에서 전체 훈련 데이터셋(배치 경사 하강법)나 하나의 샘플(확률적 경사 하강법)을 기반으로 그래디언트를 계산하는 것이 아니라 미니배치라고 부르는 작은 데이터셋 단위로 그래디언트를 계산
GPU와 같이 행렬 연산에 최적화된 하드웨어를 이용할 때 성능 향상을 얻을 수 있음
미니배치를 어느 정도 크게 하면 확률적 경사 하강법 (SGD)보다 덜 불규칙적으로 움직이고, 최솟값에 좀 더 가깝게 도달

Reference:

기계학습_하길찬 교수님 수업을 듣고 공부한 내용입니다.

← Previous Post Next Post →

선형 모델
선형회귀 학습모델