기계학습_비선형 데이터셋, 복잡도 평가 with python

7-2주차_비선형 곡선, 교차검증, 학습곡선

Posted by iheese on October 14, 2021 · 17 mins read

비선형 데이터셋에 선형회귀 모델을 적용하는 방법

  • EX) 관계식 $Y=0.5X^2+X+2+$noise ($-3\le X\le 3$)에 따라 생성된 100개의 샘플에 다항회귀 모델을 적용해보자.
import numpy as np 
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import SGDRegressor

import matplotlib.pyplot as plt 
%matplotlib inline

np.random.seed(42) #일정한 값을 위해 시드 설정

m = 100
X2 = 6 * np.random.rand(m, 1) - 3 #0~1 사이의 균인 분포에 (m,1) 행렬생성
y2 = 0.5 * X2**2 + X2 + 2 + np.random.randn(m, 1) #np.random.randn 은 가우시안 표준 정규분포에서 (m,1) 행렬 생성

plt.plot(X2, y2, "b.") #파랑색 점으로 산점도 그리기
plt.xlabel("$x_1$", fontsize=10) 
plt.ylabel("$y$", rotation=0, fontsize=10)
plt.axis([-3, 3, 0, 10]) #xmin, xmax, ymin, ymax

# 원래 속성은 x이지만, 특성벡터를 (x,x**2)으로 변환 
X2_poly = np.column_stack((X2,X2**2)) #array 형태를 세워서 두 개의 열로 붙여 행렬 만들기

# 확장된 훈련 데이터셋에 대해 선형회귀 모델 학습 
poly2_reg = LinearRegression() #모델 생성
poly2_reg.fit(X2_poly, y2) #fit() 새로운 특성벡터를 입력
poly2_reg.intercept_, poly2_reg.coef_ #편향 가중치를 출력

#학습된 결과를 그림으로 
X2_new=np.linspace(-3, 3, 100).reshape(100, 1) #(100,1) 행렬로 만들기
X2_new_poly = np.column_stack((X2_new,X2_new**2))
y2_new = poly2_reg.predict(X2_new_poly)
plt.plot(X2, y2, "b.")
plt.plot(X2_new, y2_new, "r-", linewidth=2, label="Predictions")
plt.xlabel("$x_1$", fontsize=10)
plt.ylabel("$y$", rotation=0, fontsize=10)
plt.legend(loc="upper left", fontsize=10)
plt.axis([-3, 3, 0, 10])

  • sklearn.preprocessing 의 PolynomialFeatures를 이용한 데이터셋 확장

    from sklearn.preprocessing import PolynomialFeatures
  
poly_features = PolynomialFeatures(degree=2, include_bias=False) #2차 다항식 속성을 구하는 패키지
X2_poly2 = poly_features.fit_transform(X2)
  
# 직접 확장한 데이터셋과 동일함을 확인 
(X2_poly2 == X2_poly).all()     #np.ndarray.all
  
#True


모델의 복잡도가 적절한지 판단하는 법: 교차 검증, 학습 곡선

  • 고차 다항회귀를 적용하면 선형회귀, 낮은 차수의 회귀보다 더 많은 훈련 데이터셋에 맞추려고 한다.
  • 고차 다항회귀는 과대적합될 확률이, 단순회귀적합은 과소적합될 확률이 높다. 상황에 맞는 적절한 차수를 이용해야 한다.
from sklearn.preprocessing import StandardScaler #다항식 특성으로 확장할 때 원활한 학습을 위해 스케일링 적용

for color, width, degree in (("g-", 1, 150), ("b-", 1.5, 2), ("r--", 2, 1)):
    poly_features = PolynomialFeatures(degree=degree, include_bias=False) #차수별로 다항식 회귀 만들기
    std_scaler = StandardScaler() #스케일링
    lin_reg = LinearRegression() #선형회귀
    
    X2_poly = poly_features.fit_transform(X2) #다항식 변환
    X2_poly_scaled = std_scaler.fit_transform(X2_poly) #스케일링
    lin_reg.fit(X2_poly_scaled, y2) 
    
    y2_new_pred = lin_reg.predict(std_scaler.transform(poly_features.transform(X2_new)))
    plt.plot(X2_new, y2_new_pred, color, label=str(degree), linewidth=width)

plt.plot(X2, y2, "b.", linewidth=3)
plt.legend(loc="upper left")
plt.xlabel("$x_1$", fontsize=10)
plt.ylabel("$y$", rotation=0, fontsize=10)
plt.axis([-3, 3, 0, 10])

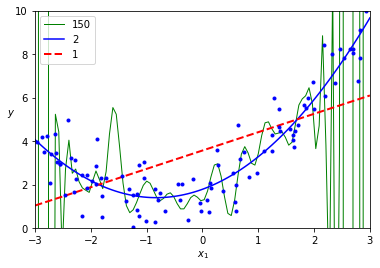
poly_features

  • 위는 2차식을 이용해 생성된 데이터셋이므로 당연한 결과지만 일반적으로는 교차검증을 이용

    • 훈련 데이터셋에서 성능은 좋은데 교차검증 점수 나쁘면 모델이 과대적합된 것
    • 훈련, 테스트셋 모두 안좋으면 과소적합된 것
    • 이 외에는 다른 방법으로는 학습 곡선을 살펴보는 것이 있다.

    학습곡선

  • 학습 곡선은 훈련 데이터셋,검증 데이터셋에 대한 성능(RMSE 또는 R^2 등)을 훈련 데이터셋의 크기(또는 학습 반복 횟수)에 대한 함수의 그래프

  • 실제로는 훈련 데이터셋에서 크기가 다른 부분 데이터셋을 만들어 모델을 여러 번 학습시키면 됨

  • 위 예에서 주어진 2차식 데이터셋이 훈련 데이터셋이라 생각하고, 훈련 데이터셋과 검증 데이터셋으로 나누어 학습 곡선을 그리는 코드를 구현해보자.
from sklearn.metrics import mean_squared_error, r2_score #MSE, R^2
from sklearn.model_selection import train_test_split #훈련용 테스트용 데이터셋 나누기 

def plot_learning_curves_pre(model, X, y):  
    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2) # 여기서 이미 무작위로 섞임
    train_mse, val_mse = [], [] 
    for m in range(2, len(X_train)+1):
        model.fit(X_train[:m], y_train[:m])
        y_train_pred = model.predict(X_train[:m])
        y_val_pred = model.predict(X_val)
        
        train_mse.append(mean_squared_error(y_train[:m], y_train_pred))
        val_mse.append(mean_squared_error(y_val, y_val_pred))
        
    plt.plot(np.sqrt(train_mse), "b-", linewidth=1, label="train")
    plt.plot(np.sqrt(val_mse), "r-", linewidth=1, label="val")
    plt.legend(loc="upper right", fontsize=10)
    plt.xlabel("Training set size", fontsize=10)
    plt.ylabel("RMSE", fontsize=10)
    
lin_reg = LinearRegression()
plot_learning_curves_pre(lin_reg, X2, y2)

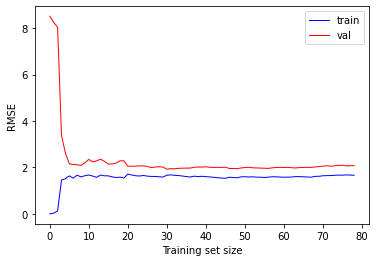
train, val

def plot_learning_curves(model, X, y, num_iter,range_y=None, metric='mse'):  
    np.random.seed(42)
    X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2) # 여기서 이미 무작위로 섞임
    train_score_mean, val_score_mean = np.zeros(len(X_train)-1), np.zeros(len(X_train)-1)
    
    if metric == "r2":
        score_ftn = r2_score  # sklearn.metrics 함수
    else:
        score_ftn = mean_squared_error   # sklearn.metrics 함수
        
    for i in range(num_iter):
        train_score, val_score = [], [] 
        for m in range(2, len(X_train)+1):
            model.fit(X_train[:m], y_train[:m])
            y_train_pred = model.predict(X_train[:m])
            y_val_pred = model.predict(X_val)
            
            train_score.append(score_ftn(y_train[:m], y_train_pred))
            val_score.append(score_ftn(y_val, y_val_pred))
            
        if metric =="r2":
            plt.plot(range(2, len(X_train)+1),train_score, "b-", linewidth=1, alpha = 0.2)
            plt.plot(range(2, len(X_train)+1),val_score, "r-", linewidth=1, alpha = 0.2)
        else:
            plt.plot(range(2, len(X_train)+1),np.sqrt(train_score), "b-", linewidth=1, alpha = 0.2)
            plt.plot(range(2, len(X_train)+1),np.sqrt(val_score), "r-", linewidth=1, alpha = 0.2)
        
        X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.2)
        train_score_mean +=train_score
        val_score_mean +=val_score
    train_score_mean = train_score_mean/num_iter
    val_score_mean = val_score_mean/num_iter
    if metric=="r2":
        plt.plot(range(2, len(X_train)+1),train_score_mean, "b-", linewidth=2, label="train")
        plt.plot(range(2, len(X_train)+1),val_score_mean, "r-+", linewidth=2, label="val")
        plt.ylabel("$R^2$", fontsize=10)
        plt.ylim((0,1))
    else:
        plt.plot(range(2, len(X_train)+1), np.sqrt(train_score_mean), "b-", linewidth=2, label="train")
        plt.plot(range(2, len(X_train)+1), np.sqrt(val_score_mean), "r-+", linewidth=2, label="val")
        plt.ylabel("RMSE", fontsize=10)
        plt.ylim(bottom=0)
    plt.legend(loc="upper right", fontsize=10)
    plt.xlabel("Training set size", fontsize=10)
    
    if range_y!=None:
        plt.ylim(top=range_y)

lin_reg = LinearRegression()
plot_learning_curves(lin_reg, X2, y2, 50, 3) #모델,X ,y ,반복 수, y범위, 기본은 mse

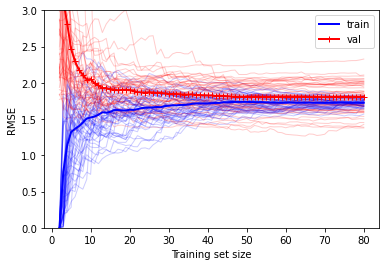
MSE 단순회귀모형

plot_learning_curves(lin_reg, X2, y2, 50, metric='r2')

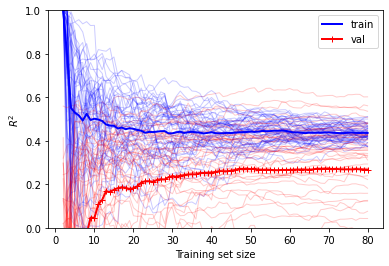
$R^2$ 단순회귀모형


단순 선형회귀 모델에 대한 학습 곡선

  • 위 결과에서 볼 수 있듯이 훈련 데이터셋의 샘플이 1~2개일 때는 모델이 완벽하게 작동하지만, 샘플 개수가 늘어남에 따라 데이터셋의 비선형성과 잡음으로 인해 완벽하게 학습하는 것이 불가능하므로 평균오차가 커지다가 어느 순간부터 평편해짐 (이 때부터는 훈련 샘플이 늘어나도 성능이 좋아지지 않음)

  • 검증 데이터셋에 대해서는 초기에는 제대로 일반화가 되지 않은 이유로 평균오차가 크다가 학습 정도가 개선됨에 따라 감소하면서 훈련 데이터셋과 가까워짐

  • 훈련 데이터셋에 대해서는 초기에는 오차가 없이 훈련을 하다가 훈련이 진행될수록 오차가 증가하다가 학습 정도가 수렴하면서 일정 수준으로 유지된다.

  • 훈련 데이터셋과 검증 데이터셋에 대한 두 학습곡선이 거의 평행해지면서 꽤 높은 오차에서 근접하는 것이 과소적합 모델의 전형적인 모습 (반드시 훈련 데이터셋에 대한 평균오차가 낮은 것은 아님)

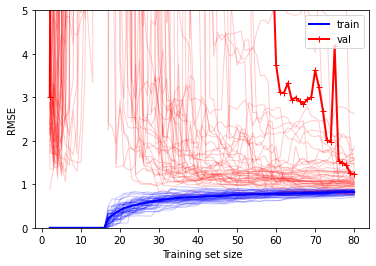
고차 다항회귀에 대한 학습 곡선

  • 아래의 그래프, 다항회귀 모델에 대한 학습 곡선을 그려보면 아래에서 보듯이 두 곡선 사이의 공간이 많이 있는데, 이것은 검증 데이터셋에 대한 성능보다 훈련 데이터셋에 대한 성능이 더 좋다는 뜻이고 과대적합 모델의 특징

  • 이 경우에도 더 큰 훈련 데이터셋을 사용하면 두 곡선이 점점 가까워짐

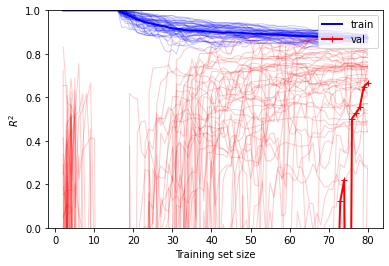
  • $R^2$을 이용하여 성능을 평가하면, 고차 다항회귀 모델의 경우에 훈련 데이터셋에 대해서는 성능이 높지만, 검증 데이터셋에 대한 성능이 낮음을 알 수 있음

과대적합이 있는 모델을 개선하는 방법

  • 모델의 복잡도를 낮추는 방법 : 이 경우에는 다항회귀 모델에서 차수를 낮추는 것

  • 훈련 샘플의 개수를 늘리는 것 : 실제로는 훈련 데이터셋을 추가로 얻는 것이 힘들 수 있음
  • 규제를 적용하는 것
poly_features = PolynomialFeatures(degree=15, include_bias=False)
std_scaler = StandardScaler()
lin_reg = LinearRegression()
    
X2_poly = poly_features.fit_transform(X2)
X2_poly_scaled = std_scaler.fit_transform(X2_poly)

plot_learning_curves(lin_reg, X2_poly_scaled, y2, 50, 5)

MSE 고차 다항회귀

$R^2$ 고차 다항회귀


Reference:

  • 기계학습_하길찬 교수님 수업을 바탕으로 공부한 내용입니다.
← Previous Post Next Post →