서포트 벡터 머신(Support Vector Machine)
-
선형이나 비선형 분류, 회귀, 이상치 탐지 등에 활용할 수 있는 매우 강력한 다목적 머신러닝 모델
-
선형 SVM 분류기 모델
- 이진분류문제에서 훈련 데이터셋 ${(\mathbf x_i,y_i):1\le i\le m}$ (단, $\mathbf x_i \in \mathbb R^n,\, y_i\in \mathbb R$)이 주어질 때, 적절한 조건을 만족하는 초평면 $\mathbf w^{\rm T}\mathbf x+b=0$를 구해서 다음과 같이 판별하는 모델
- 훈련 데이터셋의 특성벡터 $\mathbf x_i$들이 선형분리가능한 경우에 적용시킬 수 있는 하드마진 서포트벡터머신과 선형분리가능하지 않은 경우에도 적용시킬 수 있는 소프트마진 서포트벡터머신이 있음
하드마진 선형 SVM 분류모델
-
훈련 데이터셋이 선형분리가능인 경우에는 적절한 초평면 $f(\mathbf x)=b+w_1x_1+\cdots+w_nx_n=0$에 의해 레이블이 다른 샘플들을 완전히 분리시킬 수 있다.
- 위의 (아핀)함수 $f:\mathbb R^n\to \mathbb R$은 $\mathbb R^n$의 내적을 이용하면 $f(\mathbf x)=\mathbf w^{\rm T}\mathbf x+b=\langle \mathbf w,\mathbf x\rangle +b$로 쓸 수 있음
- $\mathcal P = {\mathbf x\in \mathbb R^n \mid f(\mathbf x)=0}$라 할 때, $\mathcal P$를 $\mathbb R^n$의 초평면이라 하고, $\mathbf w=(w_1,\cdots,w_n)$의 초평면에 대한 법선벡터라고 함
- $\mathbf a$와 $\mathbf b$가 $\mathcal P$의 원소이면 $0=f(\mathbf a)-f(\mathbf b)=\langle \mathbf w,\mathbf a-\mathbf b\rangle$이므로 $\mathbf a-\mathbf b$가 $\mathbf w$와 수직인 벡터
-
이때, $f(\mathbf x_i)>0$인 $\mathbf x_i$의 레이블을 $y_i = 1$, $f(\mathbf x_i)<0$인 $\mathbf x_i$의 레이블을 $y_i=-1$이라고 하면, 훈련데이터의 모든 샘플 $\mathbf x_i$에 대해
-
각 샘플 $\mathbf x_i$에서 평면까지의 거리를 평면까지의 수직거리라 할 때, 훈련 데이터 각 샘플에서 평면까지의 거리 중 최솟값을 주어진 초평면에 대한 마진(margin)이라고 함
-
주어진 훈련 데이터셋의 선형분리가능한 샘플들을 분리시키는 초평면 중에서 마진(margin)이 최대가 되는 초평면(즉, 가중치 $\mathbf w$와 절편 $b$)으로 분류기를 구성하는 것을 분류문제에 대한 하드마진(hard margin) 서포트벡터머신 모델이라고 함
-
마진이 최대가 되는 초평면의 법선벡터는 방향만이 중요하고 크기는 중요하지 않음
-
따라서 크기가 1 ($||\mathbf w||=1$)로 가정해도 되고, 이 경우 평면까지의 거리가 마진이 되는 샘플 벡터 $\mathbf x_i$에 대해 마진은 $f(\mathbf x_i)$가 됨
-
마진을 결정하는 샘플 벡터를 서포트벡터(support vector)라고 함
-
서포트벡터는 레이블이 $1$인 경우와 레이블이 $-1$인 경우에 항상 생김
-
하드마진 서포트벡터머신에서 마진이 최대(최댓값 $r$)가 되는 초평면($\mathbf w$, $b$)를 찾고 나면 훈련 데이터셋의 모든 샘플에 대해 다음이 성립 \(y_i(\langle \mathbf w,\mathbf x_i\rangle +b)\ge r,\ (1\le i \le m)\, (단, ||\mathbf w||=1)\)
-
따라서, 하드마진 서포트벡터머신의 학습 알고리즘은 다음 최적화 문제로 바뀜
\[\begin{aligned} &\quad \max_{\mathbf w, b, r} r\\ &\text{s.t }\ y_i(\langle \mathbf w,\mathbf x_i\rangle +b)\ge r,\ (1\le i\le m),\ ||\mathbf w||=1,\ r>0 \end{aligned}\]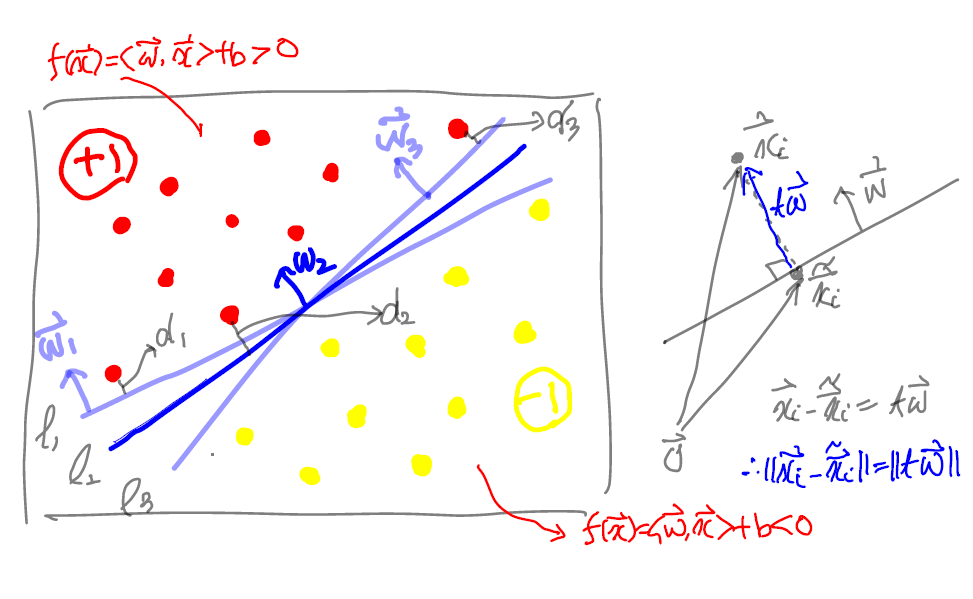
- 위 최적화문제를 변형하여 최대마진이 $r$인 서포트벡터 $\mathbf x$가 항상 $\langle \mathbf w,\mathbf x \rangle+b=1$을 만족시키도록 $\mathbf w$와 $b$를 잡는 것으로 바꾸어 생각하면(즉, $||\mathbf w||=1$ 조건을 없애고),
- $\mathbf x$를 평면에 내린 수선의 발 $\tilde{\mathbf x}$에 대해 $\mathbf x=\tilde{\mathbf x}+r \dfrac{\mathbf w}{||\mathbf w||}$이므로 조건 $\langle \mathbf w,\mathbf x\rangle+b = 1$에서
- 한편, $\tilde{\mathbf x}$은 초평면 위의 점이므로 $\langle\mathbf w,\tilde{\mathbf x}\rangle+b=0$이므로 최대마진은 $r=\dfrac 1 {||\mathbf w||}$가 된다.
-
-
하드마진 선형 SVM 분류의 학습 알고리즘 (선형분리가능인 경우)
- 설명에 의해 서포트벡터 $\mathbf x$가 $\langle \mathbf w,\mathbf x\rangle+b=1$을 만족시키는 것을 가정할 때, 선형 SVM 분류기에 대한 학습 알고리즘은 다음 최적화 문제의 해를 구하는 것으로 변형됨
-
원래 최적화 문제에서 $r=1/||\mathbf w||$의 최댓값을 구하는 것은 $||\mathbf w||$의 최솟값을 구하는 것과 같고, 다시 $||\mathbf w||^2/2$의 최솟값을 구하는 것과 같음
-
$||\mathbf w||$는 $\mathbf w=\mathbf 0$에서 미분 불가능이지만, $||\mathbf w||^2$은 모든 점에서 미분가능하므로 여러 최적화 알고리즘에서 더 잘 동작
-
위와 같이 선형적인 제약(부등식)이 있는 (아래로) 볼록한 이차 최적화문제를 Quadratic programming(QP) 문제라고 하며, QP 문제를 푸는 여러 알고리즘이 존재
- 힌지손실이라는 손실함수에 대해 서브그래디언트를 이용한 경사하강법을 적용할 수 있음 (아래 힌지손실함수 참고)
- sklearn.svm.LinearSVC`는 선형 SVM 분류 문제에 대한 최적화 알고리즘으로 Dual Cordinate Desecnt Method라고 부르는 알고리즘을 구현한 liblinear라이브러리를 사용
- 비선형 SVM 분류 문제에 적용할 수 있는
sklearn.svm.SVC는 최적화 알고리즘으로 Sequential Minimal Optimization을 구현한 libsvm 라이브러리를 기반으로 함
-
하드마진 선형 SVM 분류기를 학습시킨 후, 평면에 대한 마진 바깥부분(평면까지의 거리가 마진보다 큰)에 훈련 샘플을 추가하는 것은 SVM 분류기에 영향을 주지 않음(SVM 분류기에 영향을 주는 것은 서포트벡터)
-
SVM은 특성벡터의 스케일에 민감하므로, 학습을 시키기 전에 반드시 스케일링을 해주어야 함
소프트마진 선형 SVM 분류 모델
-
하드마진 선형 SVM의 문제점
- 선형분리가능하지 않은 데이터셋에 적용 불가
- 선형분리가 가능하더라도 이상치를 포함한 데이터셋에는 일반화 어려움
-
하드마진 SVM의 단점을 보완한 유연한 무델 필요
- 가능한 마진을 크게 잡는 것, 마진 오류(Margin violation: 샘플이 초평면과 마진 사이에 포함되는 경우)를 최소화하는 것 사이에 균형을 잡아야 함
-
마진을 크게 하는 것과 마진오류를 줄이는 것 사이의 균형을 잡기 위해 다음과 같은 최적화 문제(QP 문제)를 통해 초평면(즉, $\mathbf w,\, b$)를 구하는 것을 소프트마진 선형 SVM 분류기라고 함
-
원초문제
\[\begin{aligned} &\quad \min_{\mathbf w,b,\xi} \dfrac 1 2 ||\mathbf w||^2+C \sum_{i=1}^m \xi_i\\ &\text{s.t }\ y_i(\langle \mathbf w,\mathbf x_i\rangle +b)\ge 1-\xi_i,\qquad (1\le i \le m)\\ &\quad \ \xi_i\ge 0,\qquad (1\le i \le m) \end{aligned} \quad \cdots (2)\]
- 위 최적화 문제의 제한조건에서 각 $\xi_i\ge 0$를 각 샘플에 대한 슬랙변수(slack variable)이라 하는데, $i$번째 샘플이 마진을 얼마나 위반할 지를 나타내는 변수
- 최적화에 이용되는 알고리즘은 하드마진 SVM과 같다.
SVM 분류의 최적화 문제에 대한 쌍대문제
-
하드마진 SVM 최적화 문제와 소프트마진 SVM 최적화 문제 모두 목적함수(최소값을 구하는 대상이 되는 함수)와 부등식 제약조건의 함수가 아래로 볼록한 함수이므로 컨벡스 최적화 문제라 할 수있음
-
또, 두 문제 모두 Slater 조건을 만족하므로, 주어진 문제(원초문제)에 대한 쌍대문제 사이에 강한 쌍대성이 성립하고 KKT 조건이 성립함 (원초문제의 최솟값과 쌍대문제의 최댓값이 같아짐
- 따라서 주어진 SVM 분류와 쌍대문제에 대한 쌍대차이(dual gap)가 $0$이 되고, 쌍대문제를 해결한 후 KKT 조건을 이용하면 원초문제(SVM 분류에서의 최적화 문제)가 최소가 되는 파라미터를 구할 수 있음
-
실제 쌍대문제와 KKT 조건을 살펴보자.
\[L(\mathbf w,b,\xi,\alpha,\gamma)=\dfrac 1 2 ||\mathbf w||^2+C\sum_{i=1}^m \xi_i -\sum_{i=1}^m \alpha_i(y_i(\langle \mathbf w,\mathbf x_i\rangle+b)-1+\xi_i) -\sum_{i=1}^m \gamma_i \xi_i\]- 소프트마진 SVM 문제에 대한 라그랑주 함수는 라그랑주 승수(multiplier) $\alpha=(\alpha_1,\cdots,\alpha_m)\succeq 0$, $\gamma=(\gamma_1,\cdots,\gamma_m)\succeq 0$에 대해
- 쌍대문제는 $\alpha \succeq 0$, $\gamma \succeq 0$에 대해 $g(\alpha,\gamma)=\min_{\mathbf w,b,\xi} L(\mathbf w,b,\xi,\alpha,\gamma)$의 최댓값을 구하는 문제
-
$\min_{\mathbf w,b,\xi}L(\mathbf w,b,\xi,\alpha,\gamma)$를 구할 때, 라그랑주 함수가 $\mathbf w,b,\xi$에 대해 아래로 볼록한 함수이므로 그래디언트 벡터가 $0$이 되는 점 $\mathbf w^*,b^*,\xi^*$에서 최소가 되므로 다음이 성립
\[\begin{aligned} \dfrac{\partial L}{\partial \mathbf w} \Longrightarrow&\, \mathbf w^* =\sum_{i=1}^m \alpha_i y_i \mathbf x_i\\ \dfrac{\partial L}{\partial b} \Longrightarrow&\, \sum_{i=1}^m \alpha_i y_i=0\\ \dfrac{\partial L}{\partial \xi_i}\Longrightarrow&\, C-\alpha_i-\gamma_i=0 \ (1\le i \le m) \end{aligned}\]
-
이때, 쌍대문제의 목적함수는 $g(\alpha,\gamma)$는 다음과 같음
\[g(\alpha,\gamma)= -\dfrac 1 2 \sum_{i=1}^m\sum_{j=1}^m y_iy_j\langle \mathbf x_i,\mathbf x_j\rangle \alpha_i\alpha_j +\sum_{i=1}^m \alpha_i\] -
따라서, 소프트마진 SVM 최적화 문제에 대한 쌍대문제는 다음과 같음
-
[쌍대문제]
\[\begin{aligned} &\quad \min_{\alpha} \dfrac 1 2 \sum_{i=1}^m\sum_{j=1}^m y_iy_j\langle \mathbf x_i,\mathbf x_j\rangle \alpha_i\alpha_j -\sum_{i=1}^m \alpha_i\\ &\text{s.t }\ 0\le \alpha_i\le C,\qquad (1\le i \le m)\\ &\quad \sum_{i=1}^m y_i\alpha_i=0 \end{aligned} \quad \cdots (3)\]
-
강한 쌍대성이 성립함을 알고 있으므로, 원초문제(SVM 분류 문제)가 $\mathbf w^*, b^*, \xi^*$에서 최솟값을 가지고, 쌍대문제는 $\alpha^*,\gamma^*$에서 최댓값을 가진다고 하면
다음 KKT 조건이 성립
-
(primal feasibility 와 dual feasibility)
-
(stationary) 쌍대문제를 풀어 $\alpha^*$를 구하면 $\mathbf w^*$를 구할 수 있음
\[\mathbf w^* =\sum_{i=1}^m \alpha_i^* y_i \mathbf x_i,\quad \sum_{i=1}^m \alpha_i^* y_i=0,\quad C-\alpha_i^*-\gamma_i^*=0 \ (1\le i \le m)\] -
이때, $\alpha_i^*\neq 0$인 $i$에 대응되는 $\mathbf x_i$만이 $\mathbf w^*$에 영향을 줄 수 있는 서포트벡터
-
(complementary slackness) 모든 $1\le i \le m$에 대해 다음이 성립
\[\alpha_i^*y_i\bigl(\langle\mathbf w^*,\mathbf x_i\rangle +b^*\bigr) = \alpha_i^*(1-\xi_i^*),\quad \gamma_i^* \xi_i^*=0\] -
$\mathbf x_i$가 서포트벡터(즉, $\alpha_i\neq 0$)일 때, 다음이 성립
-
$0<\alpha_i^*<C$인 경우 $\gamma_i^*\neq 0$이므로 $\xi_i^*= 0$이 되어 $\mathbf x_i$는 마진의 경계에 위치하고 $y_i\bigl(\langle\mathbf w^*,\mathbf x_i\rangle +b^*\bigr)=1$로부터 $b^*$를 구할 수 있음
- 소프트마진 SVM 분류 문제와 비교하여 쌍대문제는 특성벡터의 차원(특성 개수)에는 상관없고, 훈련 데이터 샘플의 개수에 의존함:
- 따라서, 훈련 샘플 수가 특성의 개수보다 작을 때(예를 들어, 게놈 데이터) 원초문제를 푸는 것보다 쌍대문제를 푸는 것이 더 빠름
- SVM 분류 문제의 쌍대문제에 대한 장점: 원초문제와 달리 쌍대문제의 목적함수는 $\mathbf x_i$ 사이의 내적(유클리드 내적)을 이용하여 표현되어 있으므로 이 내적을 일반적인 내적으로 확장하여 비선형문제에도 적용시킬 수 있음 (다음 포스트 비선형 SVM 분류참고)
SVM 분류에서의 최적화 문제를 SVM 분류기에 대한 손실함수 관점에서 해석
-
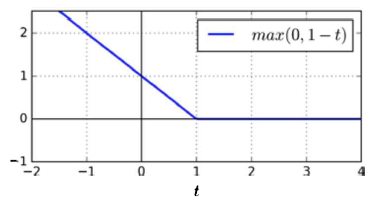
힌지손실(hinge loss)함수 $\max{0,1-t}$: $t=1$을 제외하면 미분가능하고 아래로 볼록한 함수($t=1$에서의 서브그래디언트벡터는 $[-1,0]$)이므로 서브그래디언트 벡터를 이용한 경사하강법이 가능
-
힌지손실(hinge loss)함수에 대한 최솟값을 구하는 문제 $\min_t\max{0,1-t}$는 다음 최적화 문제와 동치임
\[\begin{aligned} & \min_{\xi, t}\xi \\ \text{s.t } & \xi \ge 0\\ & \xi \ge 1-t \end{aligned}\] -
따라서 소프트 마진 SVM 문제의 손실함수는 다음과 같이 생각할 수 있다.
\[J(\mathbf w,b)=\dfrac 1 2 ||\mathbf w||_2^2 +C\sum_{i=1}^m \max\{0,1-y_i(\langle \mathbf w,\mathbf x_i\rangle+b)\}\] -
힌지손실함수 입장에서 보면 $||\mathbf w||^2$은 규제 항(패널티 항)으로 볼 수 있으므로, $C$는 릿지회귀에서의 규제 하이퍼파라미터 $\alpha$와 비교하여 역수의 역할을 함을 이해할 수 있음
- SVM 모델이 과대적합이라면 $C$를 감소시켜 모델을 규제할 수 있음
-
즉, SVM 분류문제에서 마진을 최대화하는 것을 힌지손실함수를 통해 해석하면 규제를 가하는 것으로 해석할 수 있음
Reference:
-
기계학습_하길찬 교수님 수업을 듣고 공부한 내용입니다.
- 서포트 벡터 머신_ 생각정리
- 서포트 벡터 머신_excelsior