비선형 SVM 분류와 커널 (Kernel) SVM 분류 모델
1. 비선형 SVM 분류
- 선형적으로 분류할 수 없는 비선형 데이터셋이 주어질 때, 선형회귀 모델에서 다루었던 것처럼 다항 특성, 다른 비선형 특성 추가해서 선형 SVM 모델을 학습시키는 것이 가능
- 낮은 차수 다항식은 복잡한 데이터셋을 설명하는데 어려움이 있고 높은 차수 다항식 특성은 많은 특성은 추가해야 하기 때문에 모델 학습 시간이 오래 걸림
2. 커널과 커널 트릭
- 소프트마진 SVM 최적화 문제에 대한 쌍대문제
-
SVM 분류의 학습 문제와 동등한 쌍대문제인 위 식(3)을 보면, 실제로 계산에 필요한 것은 특성벡터 사이의 내적 $\langle \mathbf x_i,\mathbf x_j\rangle$이 중요하며, 이 내적을 특성벡터의 차원과 상관없이 효율적으로 계산할 수 있으면 앞에서 언급한 특성 추가시의 문제점을 해결할 수 있음
-
예를 들어, 주어진 샘플 벡터가 $\mathbf x = (x_1,x_2)^{\rm T}$일 때, 이차다항식 특성벡터를 $\phi(\mathbf x)=(x_1^2,x_2^2,\sqrt 2 x_1x_2,\sqrt 2 x_1,\sqrt 2 x_2,1)^{\rm T}$와 같이 생성하고, 새로 얻은 특성벡터 사이의 내적을 계산하면 (단, $\mathbf x_i = (x_{i1},x_{i2})^{\rm T})$
\[\langle \phi(\mathbf x_i),\phi(\mathbf x_j)\rangle = x_{i1}^2x_{j1}^2+x_{i2}^2x_{j2}^2+2x_{i1}x_{i2}x_{j1}x_{j2}+2x_{i1}x_{j1}+2x_{i2}x_{j2}+1\\=(\langle\mathbf x_i,\mathbf x_j\rangle +1)^2\]-
$\mathbf x_i$로부터 새로운 특성벡터를 생성하는 함수를 특성맵(feature map)이라고 함
-
위의 예에서, (편차제외하고 5차원 벡터) $\phi(\mathbf x_i)$와 $\phi(\mathbf x_j)$를 직접 구하지 않더라도(즉, 특성맵을 구하지 않더라도) 2차원 벡터에 대한 $\langle\mathbf x_i,\mathbf x_j\rangle$의 함수 $K(\mathbf x_i,\mathbf x_j):=(\langle \mathbf x_i,\mathbf x_j\rangle+1)^2$을 이용하면 식 (3)에서 특성벡터 $\phi(\mathbf x_i)$에 대한 SVM을 적용시킬 수 있음
-
일반적으로 $d$차 다항 특성벡터에 대한 대한 내적 $\langle\phi(\mathbf x_i),\phi(\mathbf x_j)\rangle$는 $\phi(\mathbf x_i)$를 구하지 않더라도 $K(\mathbf x_i,\mathbf x_j):=(\langle \mathbf x_i,\mathbf x_j\rangle+1)^d$와 같이 계산할 수 있음
- 이때, 함수 $K(\mathbf x_i,\mathbf x_j):=(\langle \mathbf x_i,\mathbf x_j\rangle+1)^d$를 $d$차 다항식 커널(kernel)이라고 함
- 이처럼 커널을 이용하여 특성벡터를 직접 구하지 않고, SVM 분류기를 학습시키는 방법을 커널 트릭(kernel trick)이라고 함
-
-
3. 일반적인 커널
- 일반적으로 연속함수 $K:\mathbb R^n\times \mathbb R^n\to \mathbb R$에 대해 다음 두 조건을 만족할 때 커널이라고 함
(조건 1) 임의의 두 벡터 $\mathbf x,\mathbf z\in \mathbb R^n$에 대해 $K(\mathbf x, \mathbf z) = K(\mathbf z, \mathbf x)$
(조건 2) 모든 자연수 $m$에 대해, $m$개의 벡터 $\mathbf x_1,\cdots,\mathbf x_m$와 $m$개의 실수 $c_1,\cdots,c_m$이 임의로 주어질 때,
\[\sum_{i=1}^m\sum_{j=1}^m K(\mathbf x_i,\mathbf x_j)c_ic_j\ge 0\]
- $K:\mathbb R^n\times \mathbb R^n\to \mathbb R$가 위 조건을 만족하는 커널이면
적당한 힐버트 공간 $\mathcal H$와 특성함수 $\phi:\mathbb R^n\to \mathcal H$가 존재해서
\[K(\mathbf x,\mathbf z)=\langle \phi(\mathbf x),\phi(\mathbf z)\rangle_{\mathcal H}\]가 성립함을 보일 수 있고, SVM에 적용할 수 있음 (힐버트 공간이란 완비성을 만족하는 내적공간)
4. 커널 SVM
-
SVM에서 특성벡터를 직접 구하는 대신 커널 $K$에 대한 커널 트릭을 사용하여 다음과 같이 SVM 최적화 문제의 쌍대문제를 해결하고 이를 통해 SVM 분류기 예측을 수행하는 모델을 커널 SVM 모델이라고 함
-
커널 SVM 쌍대문제
\[\begin{aligned} &\quad \min_{\alpha} \dfrac 1 2 \sum_{i=1}^m\sum_{j=1}^m y_iy_j K(\mathbf x_i,\mathbf x_j) \alpha_i\alpha_j -\sum_{i=1}^m \alpha_i\\ &\text{s.t }\ 0\le \alpha_i\le C,\qquad (1\le i \le m)\\ &\quad \sum_{i=1}^m y_i\alpha_i=0 \end{aligned} \quad\] -
SVM에서 자주 사용하는 커널
- 선형 커널 : $K(\mathbf x,\mathbf z)=\mathbf x^{\rm T}\mathbf z$
- $d$차 다항식 커널 : $K(\mathbf x,\mathbf z)=(\gamma \mathbf x^{\rm T}\mathbf z +r)^d$, $(\gamma,\, r\in \mathbb R)$
- 가우시안 RBF(Radial Basis Function) : $K(\mathbf x,\mathbf z)=\exp(-\gamma|| \mathbf x-\mathbf z||^2)$
- 시그모이드 : $K(\mathbf x,\mathbf z)=\text{tanh}(\gamma \mathbf x^{\rm T}\mathbf z + r)$
-
커널 SVM에서 예측하는 방법: 편차 $b^*$는 구할 수 있지만 모델 파라미터 $\mathbf w^*$는 직접 구할 수 없는 상황
\[\begin{aligned} \langle \mathbf w^*,\phi(\mathbf x)\rangle+b^*= &\langle \bigl(\sum_{i=1}^m \alpha^*y_i\phi(\mathbf x_i)\bigr),\phi(\mathbf x)\rangle+b^*\\ =& \sum_{i=1}^m \alpha^*y_i \langle \phi(\mathbf x_i),\phi(\mathbf x)\rangle +b^*\\ =& \sum_{i=1}^m \alpha^*y_i K(\mathbf x_i,\mathbf x) +b^* \end{aligned}\]
커널 SVM에서 학습 알고리즘은 선형 SVM의 쌍대문제에서 특성 맵 $\phi$을 통해 구체적인 특성벡터 $\phi(\mathbf x)$사이의 내적을 계산하는 대신 커널 트릭을 이용하는 것이므로 최적해를 주는 $\alpha^*$를 구할 수 있지만, 이로부터 원초문제의 $\mathbf w^*$를 구하면 KKT 조건_ stationary에 의해
\[\mathbf w^* = \sum_{i=1}^m \alpha_i^*y_i\phi(\mathbf x_i)\]가 되어 특성 맵을 모르면 $\mathbf w^*$를 구할 수 없다. (실제로 $\mathbf w^*$는 특성벡터 $\phi(\mathbf x_i)$와 같은 차원이어야 함)
하지만, 주어진 샘플 벡터 $\mathbf x$에 대한 예측은
이므로 상수 $b^*$만 구할 수 있으면 $\mathbf w^*$를 직접 구하지 않고도 예측을 할 수 있음
실제로 편차 $b^*$는 $x_I$가 서포트벡터머신일 때 $0<\alpha_i^*<C$인 $i$에 대해
\[y_i\bigl(\langle \mathbf w^*,\phi(\mathbf x_i)\rangle+b^*\bigr)=1\]\[\sum_{\substack{i=1\\ 0<\alpha^*_i<C}}^m \bigl(y_i-\langle \mathbf w^*,\phi(\mathbf x_i)\rangle\bigr) = n_s b^*\]
이 성립하므로 ${i 1\le i\le m, 0<\alpha_i^*<C}$의 원소의 개수를 $n_s$라 할 때, 가 되고, 이로부터 다음과 같이 $b^*$를 구할 수 있음
\[b^* = \dfrac 1{n_s} \sum_{\substack{i=1\\0<\alpha_i^*<C}}^m\left(y_i - \sum_{j=1}^m \alpha_j^* y_j K(\mathbf x_j,\mathbf x_i)\right)\](위 등식에서 $\sum_{j=1}^m$은 $\sum_{\substack{j=1 \ 0<\alpha_j^*\le C}}^m$과 같아짐에 주목)
서포트벡터머신 분류 모델 (sklearn의 사용가능한 클래스)
- 소프트마진 선형 SVM 분류기에 대한
sklearn의 클래스들
- 손실함수 (커널 SVM 쌍대문제)의 최솟값을 효율적으로 구하는 최적화 알고리즘(liblinear 라이브러리)을 구현한
sklearn.svm모듈의LinearSVC클래스 (API)
커널 트릭을 지원하지 않지만, 훈련 시간 복잡도는 샘플 수 $m$과 특성 수 $n$에 대해 대략 $O(m\times n)$
LinearSVC는 규제에 편향을 포함시켜 구현되어 있으므로, 훈련 데이터셋에서 평균을 빼서 변형한 데이터셋의 평균이 $0$이 되도록 조절해야 함(보통StandardScaler를 통해 스케일링을 해야 하므로 이 문제는 해결됨)loss의 기본값이 “squared_hinge”로 설정되어 있으므로loss="hinge"로 설정해주어야 함- 훈련 샘플보다 특성의 개수가 많으면
dual=True로 설정하여 쌍대문제를 풀고, 훈련 샘플이 더 많은 경우는dual=False로 설정하여 성능을 조절
- 손실함수 의 최솟값을 구하기 위해 서브그래디언트에 대한 경사하강법을 사용하는
sklearn.linear_model모듈의SGDClassifier(loss="hinge", alpha=1/(m*C))클래스 (API)
- 손실함수를 “hinge”로 설정하고 규제 하이퍼파라미터는
alpha는C의 역수이므로 위와 같이 설정(m은 샘플 수)LinearSVC보다 빠르지 않지만, 데이터셋이 아주 커서 메모리에 적재할 수 없거나, 온라인 학습으로 분류문제를 다룰 때 유용- 이 경우에도 스케일링이 필요함
- 커널 트릭을 이용하여 SVM 분류에 대한 쌍대문제를 푸는 알고리즘(libsvm 라이브러리 기반)을 구현한
sklearn.svm모듈의SVC클래스를 이용하여SVC(kernel="linear")로 모델 객체를 생성 (API)
훈련 시간의 복잡도는 샘플 수 $m$과 특성 수 $n$에 대해 대략 $O(m^2\times n)$과 $O(m^3\times n)$사이
다항식 커널 $K(\mathbf x,\mathbf z)=(\gamma \mathbf x^{\rm T}\mathbf z +r)^d$을 사용하는 커널 SVM 분류기 모델의 대표적인 예 :
SVC(kernel="poly", degree=3, gamma="scale", coef0=1, C=5)와 같은 형태로 객체 생성(
degree,gamma,coef0는 각각 커널식에서 $d$, $\gamma$, $r$에 대응되는 입력변수) [API 참고]가우시안 RBF 커널 $K(\mathbf x,\mathbf z)=\exp(-\gamma||\mathbf x-\mathbf z||^2)$을 사용하는 커널 SVM 분류기 모델 :
SVC(kernel="rbf", gamma=5, C=5)와 같은 형태로 객체 생성 (gamma는 커널식에서 $\gamma$에 대응되는 입력변수) [API 참고]
서포트벡터머신 회귀
-
서포트벡터머신은 선형, 비선형 분류 뿐만 아니라 선형, 비선형 회귀 문제에도 이용할 수 있음
-
$\epsilon>0$과 훈련 데이터셋 ${(\mathbf x_1,y_1),\cdots,(\mathbf x_m,y_m)}$이 주어질 때, 선형 서포트벡터머신 회귀는 선형함수 $f(\mathbf x)=\langle \mathbf w,\mathbf x\rangle +b$ 중에서 $|y_i-f(\mathbf x_i)| \le \epsilon, (1\le i\le m)$이 되는 $\mathbf w,b$를 구하는 모델 (여기서 $\epsilon$은 마진에 해당)
- 위에서 기술한 목표는 하드마진 SVM 회귀문제에 해당
- 실제로는 위 조건(모든 $i=1,\cdots,m$)을 만족하는 $f(\mathbf x)$를 구할 수 없는 경우가 있으므로 소프트마진 SVM 회귀문제는 조건을 완화하여
을 만족하는 $\mathbf w,b$를 찾는 문제를 생각 ($\xi_i$와 $\xi_i’$은 슬랙변수)
-
즉, 분류 문제와는 반대로 제한된 마진오류 내에서 마진 경계사이에 최대한 많은 샘플이 포함되도록 학습
-
소프트마진 SVM 회귀문제를 규제항을 포함하여 힌지손실함수로 나타내면 다음과 같음
\[\min_{\mathbf w,b}\left(\dfrac 1 2 ||\mathbf w||^2 + C\sum_{i=1}^m \max\bigl(0, |y_i-\langle \mathbf w,\mathbf x_i\rangle|-\epsilon\bigr)\right)\quad\] -
위 손실함수를 최소화하는 것을 소프트마진 SVM 회귀 문제로 표현하면
- 위 원초문제도 컨벡스 최적화 문제이고 Slater 조건을 만족하므로 강한 쌍대성이 만족되고, 쌍대문제를 구하고 나면 소프트마진 SVM 분류의 경우처럼 커널 트릭을 이용한 커널 SVM 회귀모델을 구성하는 것도 가능 (보다 자세한 내용은 링크를 참고)
서포트벡터머신 회귀 모델(sklearn의 사용가능한 클래스)
-
SVM 분류기를 생성하는
LinearSVC클래스의 회귀 버전에 해당하는sklearn.svm모듈의LinearSVR클래스 (API) -
커널 SVM 분류기를 생성하는
SVC클래스의 회귀 버전에 해당하는sklearn.svm모듈의SVR클래스 (API) -
LinearSVR
은 훈련 데이터셋의 크기에 비례해서 선형적으로 학습 시간이 늘어나지만,SVR`은 훨씬 느려짐에 유의
서포트 벡터머신에 대한 Scikit-learn의 클래스들
-
서포트벡터머신의 모델은 모두 특성벡터의 스케일에 민감하므로, 학습을 시키기 전에 스케일링을 하는 것을 기억
-
sklearn.linear_model모듈의 확률적 경사하강법을 이용한 선형 서포트벡터머신 모델:
- 회귀:
SGDRegressor(loss="epsilon_insensitive")또는SGDRegressor(loss="squared_epsilon_insensitive")(API)- 분류:
SGDClassifier(loss="hinge")또는SGDRegressor(loss="squared_hinge")(API)- 확률적 경사하강법으로 구현된 위의 클래스를 이용하여 생성된 SVM 모델의 객체에 대해서는 규제(regularization)에 대한 하이퍼파라미터가
alpha(C와 역수관계임에 유의, alpha가 커지면 규제가 커지고, alpha가 작아지면 규제가 작아짐)
-
sklearn.svm모듈의 선형 서포트벡터머신 모델:liblinear라이브러리를 이용한 최적화 알고리즘 사용-
회귀:
LinearSVR(API)- 손실함수의 기본값인
loss="epsilon_insensitive"를 사용하면 $\ell_1$ 규제를 사용, $\ell_2$ 규제를 사용하려면loss="squared_epsilon_insensitive"로 설정
- 손실함수의 기본값인
-
분류:
LinearSVC(API)- 기본적인 선형 서포트벡터머신 분류기를 사용하려면
loss="hinge"로 설정 (기본값은 “sqaured_hinge”)
- 기본적인 선형 서포트벡터머신 분류기를 사용하려면
-
규제 하이퍼파라미터는
C임에 주의(C가 커지면 규제가 작아지고, C가 작아지면 규제가 커짐) -
서포트벡터 모델에서의 최적화 문제에 대한 쌍대문제를 이용할 지를 결정하는 클래스 입력변수는
dual- 기본값은
dual=True - 일반적으로 샘플의 개수가 특성벡터의 개수보다 많을 때는
dual=False로 설정하는 것이 효율적
- 기본값은
-
-
sklearn.svm모듈의 (커널) 서포트벡터머신 모델:libsvm라이브러리를 이용한 최적화 알고리즘 사용- 기본적으로 커널 서포트벡터머신 모델에서 쌍대문제에 대한 최적화를 하는 것이므로 훈련 데이터 샘플의 개수가 너무 많으면 비효율적임
- 훈련 샘플의 개수가 수만개를 넘는 경우에는 비효율적일 수 있음
-
회귀에 사용되는
SVR(API)과 분류에 사용되는SVC(API)가 있음SVC을 이용하여 3종류 이상의 레이블을 갖는 다중분류 문제를 해결하는 전략을 선택하는 변수는decision_function_shape- 일대다 전략은
decision_function_shape="ovr", 일대일 전략은decision_function_shape="ovo"로 선택 - 레이블의 종류가 많은 경우에는 “ovo” 전략이 효율적일 수 있음
- 학습된 객체의 속성
support_를 이용하면 서포트벡터의 index를 구할 수 있고, 속성support_vectors_를 이용하면 서포트벡터를 구할 수 있음
-
입력변수
kernel을"linear"로 설정하면 쌍대문제를 이용한 선형 서포트벡터머신 모델kernel로 선택할 수 있는 기본적인 커널함수는 “linear”, “poly”, “rbf”, “sigmoid”
-
사용자가 새롭게 정의한 커널을 사용하는 두 가지 방법이 있음 (자세한 내용은 다음 reference를 읽고 확인할 것, 참고할 예제링크)
- 조건을 만족하는 커널함수를 파이썬에서 mykernel로 정의한 후
kernel=mykernel과 같이 전달(문자열이 아닌 함수이름으로 전달하는 것이 주목)하는 방법 - 새롭게 정의한 커널함수 $K$를 이용하여 $m$개의 훈련 샘플에 대한 $m\times m$ Gram 행렬 $(K(\mathbf x_i, \mathbf x_j))$을 미리 계산하고,
kernel="precomputed"로 설정한 다음 객체를 학습시킬 때fit()에 대한 입력으로 훈련데이터셋에 행렬 대신, 계산된 Gram 행렬을 전달
- 조건을 만족하는 커널함수를 파이썬에서 mykernel로 정의한 후
MNIST 데이터셋을 이용한 실습
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784', version=1)
mnist.keys()
#dict_keys(['data', 'target', 'frame', 'categories', 'feature_names', 'target_names', 'DESCR', 'details', 'url'])
print(mnist['DESCR']) # 데이터셋 설명
X, y = mnist["data"], mnist["target"]
print(X.shape, y.shape)
type(y[0])
#(70000, 784) (70000,)
#str
y = y.astype(np.uint8) #0~255 정수화
4와 나머지 숫자를 구분하는 서포트벡터머신 분류기
-
데이터셋을 훈련 데이터셋과 테스트 데이터셋으로 나누고
-
레이블이 4인 것은 1, 4가 아닌 것은 0으로 수정한 후 학습
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:] y_train_4 = (y_train == 4) y_test_4 = (y_test == 4) y_train_4[:10].astype(np.uint8) # 0 OR 1
1. SGDClassifier를 이용한 SVC 생성과 교차검증을 이용한 성능 측정
- $k$-겹 교차검증에 대한 score만 구할 때:
sklearn.model_selection.cross_val_score이용 - $k$-겹 교차검증에 대한 예측값이 필요할 때:
sklearn.model_selection.cross_val_predict이용
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(loss="hinge", random_state=123)
from time import time #얼마나 걸리는지 보기 위해
start = time()
print(cross_val_score(sgd_clf, X_train, y_train_4, cv=3, scoring="accuracy"))
time()-start
#[0.9763 0.9735 0.95655]
#26.294976234436035
#정밀도
start = time()
print(cross_val_score(sgd_clf, X_train, y_train_4, cv=3, scoring="precision"))
time()-start
#[0.86769845 0.84177521 0.70243902]
#24.624820232391357
#재현율
start = time()
print(cross_val_score(sgd_clf, X_train, y_train_4, cv=3, scoring="recall"))
time()-start
#[0.89265537 0.89625064 0.96098563]
#24.25176739692688
#스케일링 후 정확도
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train.astype(np.float64))
start = time()
print(cross_val_score(sgd_clf, X_train_scaled, y_train_4, cv=3, scoring="accuracy"))
time()-start
#[0.97885 0.97695 0.98005]
#53.56697106361389
2. SVC(kernel=”rbf”) 를 이용한 SVC 생성과 교차검증을 이용한 성능 측정
- 샘플의 개수(60000개)가 특성 수(784개) 보다 큰 경우:
LinearSVC(dual=False)보다 시간이 많이 걸림
from sklearn.svm import SVC
svm_clf = SVC(kernel="rbf")
start = time()
print(cross_val_score(svm_clf, X_train_scaled, y_train_4, cv=3, scoring="accuracy", n_jobs=-1))
time()-start
#[0.9926 0.99085 0.99215]
#370.1666090488434
3. SVC(kernel=”rbf”, decision_function_shape=”ovo”)을 이용한 다중 분류기
- 레이블이 0, 3, 4인 데이터 샘플만 추려서 3개의 클래스에 대한 분류를 실습
- OvR 전략을 선택하는 경우 학습에 사용되는 훈련데이터 개수는 대략 30000개, 예측기 3개
- OvO 전략을 선택하는 경우 학습에 사용되는 훈련데이터 개수는 대략 12000개, 6개
label0 = (y_train==0)
label3 = (y_train==3)
label4 = (y_train==4)
idx = label0 | label3 | label4
X_train_red = X_train_scaled[idx]
y_train_red = y_train[idx]
svm3_clf = SVC(kernel="rbf", decision_function_shape="ovo")
svm3_clf.fit(X_train_red, y_train_red)
# 학습된 다중(3개 클래스) 분류기에 대한 예측값과 실제값 비교
print(svm3_clf.predict([X_train_red[4:10]]))
print(y_train_red[4:10])
# 학습된 객체의 decision_function을 이용하면 각 샘플마다 각 클래스에 속할 score를 반환함
some_digit_score = svm3_clf.decision_function(X_train_red[4:5])
print(some_digit_score)
# 학습된 분류기 객체는 classes_ 속성에 레이블을 값으로 정렬하여 저장함
svm3_clf.classes_
# 위에서 구한 score가 가장 높은 인덱스에 대응되는 클래스를 svm3_clf.classes_에서 읽으면 예측값
result_id = np.argmax(some_digit_score)
print(svm3_clf.classes_[result_id])
print(y_train_red[4])
3. 커널 SVC 실습
- xor 연산과 관련된 데이터셋
- 퍼셉트론의 한계, 다층 신경망의 유용함을 보여준 예
np.random.seed(0)
X = np.random.randn(200, 2)
y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
y = y.astype(np.uint8)
plt.scatter(X[y == 1, 0], X[y == 1, 1],
c='b', marker='o', label='label1', s=10, alpha=0.8)
plt.scatter(X[y == 0, 0], X[y == 0, 1],
c='r', marker='s', label='label0', s=10, alpha=0.8)
plt.legend()
plt.xlabel(r"$x_1$")
plt.ylabel(r"$x_2$")
plt.show()
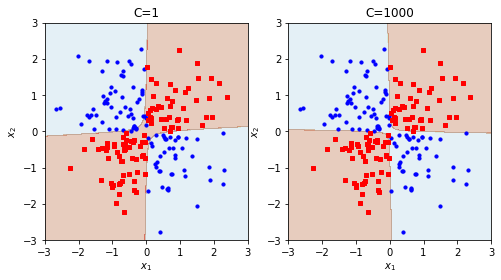
# 2차 다항식 커널을 이용한 SVC모델 (xy 항이 생기므로 분리가능)
poly_svm_clf = SVC(kernel="poly", degree=2)
poly_svm_clf.fit(X,y)
poly_svm_clf1000 = SVC(kernel="poly", degree=2, C=1000)
poly_svm_clf1000.fit(X,y)
import matplotlib as mpl
def plot_xor(x1, x2, model, title=None, x1min=-3, x1max=3, x2min=-3, x2max=3):
xx1, xx2 = np.meshgrid(np.linspace(x1min, x1max,1000),
np.linspace(x2min, x2max,1000))
zz = np.reshape(model.predict(
np.array([xx1.ravel(), xx2.ravel()]).T), xx1.shape)
plt.contourf(xx1, xx2, zz, cmap=mpl.cm.Paired_r, alpha=0.3)
y = np.logical_xor(x1 > 0, x2 > 0)
plt.scatter(x1[y], x2[y], c='b',
marker='o', label='label:1', s=10)
plt.scatter(x1[~y], x2[~y], c='r',
marker='s', label='label:0', s=10)
plt.xlim(x1min, x1max)
plt.ylim(x2min, x2max)
plt.title(title)
plt.xlabel(r"$x_1$")
plt.ylabel(r"$x_2$")
plt.figure(figsize=(8,4))
plt.subplot(121)
plot_xor(X[:,0],X[:,1],poly_svm_clf, title="C=1")
plt.subplot(122)
plot_xor(X[:,0],X[:,1],poly_svm_clf1000, title="C=1000")
Reference:
-
기계학습_하길찬 교수님 수업을 듣고 공부한 내용입니다.