기계학습_결정트리(Decision Tree)

13주차_결정트리의 분할 규칙, 손실함수, 계산 복잡도

Posted by iheese on November 16, 2021 · 12 mins read

결정트리 (Decision Tree)

  • 서포트벡터머신처럼 분류와 회귀작업, 다중출력도 가능한 머신러닝 알고리즘으로 최근에 자주 사용되는 강력한 머신러닝 알고리즘 중 하나인 랜덤포레스트(Random Forest)의 기본 구성 요소

    • 트리구조를 생성할 때, 각 노드의 자식노드가 3개 이상인 것을 허용하는 트리를 생성할 수도 있지만, 대개 자식노드가 2개인 이진트리를 사용
    • scikit-learn은 이진트리를 생성하는 CART 알고리즘을 사용 (셋 이상의 자식노드를 생성하는 ID3과 같은 알고리즘도 있음)
    • 서포트벡터머신의 경우와 달리 (특성의 평균을 원점으로 하고, 특성의 스케일을 맞추는) 스케일링이 거의 필요없음


기본적인 아이디어

  • 결정트리를 하향식(top-down)으로 구성하는 기본적인 아이디어
  • 훈련데이터셋 $D={(\mathbf x_i,y_i)|1\le i \le m}$의 특성벡터 $\mathbf x_i\, (1\le i \le m)$를 포함하는 특성공간 $\mathcal X$를 어떤 분할규칙(splitting rule)에 따라 겹치지 않는 작은 영역 $\mathcal R_i$로 $ \mathcal X = \mathcal R_1 \cup \mathcal R_2 \cup \cdots \cup \mathcal R_N $

과 같이 나누고,

  • 회귀문제인지 분류문제인지에 따라, 임의의 샘플벡터 $\mathbf x$에 대해 다음과 같이 예측

  • 회귀의 경우: 샘플 $\mathbf x$가 속하는 작은 영역 $\mathcal R_i$에 대해, 이 영역에 속하는 훈련샘플 $\mathbf x_j$의 $y_j$값의 평균으로 예측 $ \hat y = \dfrac 1 {r_i} \sum_{\mathbf x_j \in \mathcal R_i}y_j, \quad (r_i=\bigl|{(\mathbf x_j,y_j)\in D|\mathbf x_j\in \mathcal R_i}\bigr|) $

  • 분류의 경우: 샘플 $\mathbf x$가 속하는 작은 영역 $\mathcal R_i$에 대해, $\mathcal R_i$에 속하는 훈련샘플에 대한 레이블 중 가장 많이 나타나는 레이블

  • 예를 들어, 앞서 살펴본 붓꽃 데이터에서 특성 $x_1$=”꽃잎 길이(petal length)”는 $1.0\le x_1\le 6.9$사이의 값을 가지고, 특성 $x_2$=”꽃잎너비(petal width)”는 $0.1\le x_2\le 2.5$ 사이의 값을 가짐.

  • 따라서 특성공간 $\mathcal X=\{(x_1,x_2) \mid 1.0\le x_1\le 6.9,\ 0.1\le x_2 \le 2.5\}$

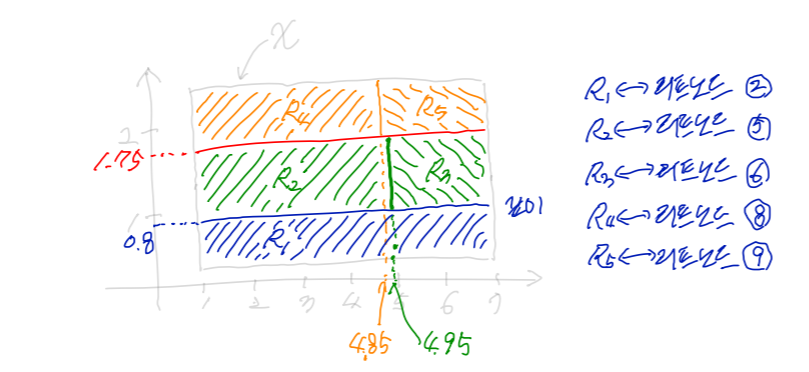
  • 두 특성을 이용하여 만든 깊이가 3인 결정트리 그림이 다음과 같을 때,

    iris_tree

    각 영역 $\mathcal R_i$는 리프노드(leaf node)에 의해 결정 됨

    iris_tree2

  • 예를 들어, 그림에서 리프노드 2에 대응되는 영역을 $\mathcal R_1$, 리프노드 5에 대응되는 영역을 $\mathcal R_2$라 하면 $ \mathcal R_1={(x_1,x_2)\,\in \, \mathcal X\, |\, x_2 \le 0.8},\quad \mathcal R_2={(x_1,x_2)\, \in \, \mathcal X\,|\, 0.8<x_2 \le 1.75,\, x_1\le 4.95} $ 이고, $\mathcal R_2$에 속하는 훈련샘플 중 레이블이 setosa인 것은 $0$개, versicolor인 것은 $47$개, viginica인 것은 $1$개이므로 $\mathcal R_2$ 영역에 속하는 샘플에 대해서는 레이블이 versicolor인 것으로 예측


결정트리의 분할규칙, 손실함수

  • 이진트리(Binary Tree)

    • 노드(node)와 변(edge)으로 구성된 그래프의 일종으로 각 노드는 자식노드(child node)를 갖지 않거나 두 개의 자식노드를 가짐
    • 보통 위에서 아래로 가지치는 형태, 또는 왼쪽에서 오른쪽으로 가지치는 형태로 나타냄
    • 맨 처음 시작하는 노드를 루트노드(root node)라 부르고, 자식노드를 갖지 않는 노드를 리프노드(leaf node)라고 부름

  • 결정트리의 예측함수: 훈련데이터셋 $D=\{(\mathbf x_i,y_i) | 1\le i \le m\}$의 특성벡터 $\mathbf x_i\, (1\le i \le m)$를 포함하는 특성공간 $\mathcal X$의 임의의 부분집합 $\mathcal A\subset \mathcal X$에 대해, 다음과 같이 정의

    • 집합 $\mathcal A$에 속하는 훈련샘플의 개수를 $n_{\mathcal A}$. 즉, $n_{\mathcal A}=| \{(\mathbf x_j,y_j)\in D|\mathbf x_j\in \mathcal A\} |$

    • 지시함수(indicator function) $\mathbf 1_{\mathcal A}$를 다음과 같이 정의

      $ \mathbf 1_{\mathcal A}(\mathbf x)=\begin{cases} 1 & \ \text{if } \mathbf x\in \mathcal A\ 0 &\ \text{if }\mathbf x \notin \mathcal A\end{cases} $

    • 회귀문제의 경우, 집합 $\mathcal A$에서 정의된 상수함수 $g^{\mathcal A}$를 다음과 같이 정의

      $ g^{\mathcal A}(\mathbf x) = \dfrac 1 {n_{\mathcal A}} \sum_{i=1}^m y_i\mathbf 1_{\mathcal A}(\mathbf x_i) ,\ (\mathbf x\in \mathcal A) $

    • 레이블이 ${1,2,\cdots,K}$인 분류문제의 경우, 집합 $\mathcal A$에 속하는 훈련 샘플의 레이블 중 레이블이 $k$인 것의 비율을 $p_k^{\mathcal A}$ 즉,

      \[p_k^{\mathcal A} = \dfrac 1 {n_{\mathcal A}} \sum_{i=1}^m \mathbf 1_{\{k\}}(y_i)\mathbf 1_{\mathcal A}(\mathbf x_i)\]

    라 할 때, $\mathcal A$에서 정의된 상수함수 $g^{\mathcal A}$를 다음과 같이 정의

    $ g^{\mathcal A}(\mathbf x)= \text{argmax}_{\substack{k\in {1,\cdots,K}}}p_k^{\mathcal A}, \ (\mathbf x\in \mathcal A) $

    • 훈련 데이터셋 $D={(\mathbf x_i,y_i) | 1\le i \le m}$으로부터 학습된 결정트리에 대해 특성공간 $\mathcal X$가 서로 겹치지 않는 작은 영역 $\mathcal R_i$ $(1\le i \le N)$로 다음

      \[\mathcal X = \mathcal R_1 \cup \mathcal R_2 \cup \cdots \cup \mathcal R_N\]

      과 같이 분할되었다면, 이 결정트리에 대한 예측함수 $g$는 앞에서 정의한 상수함수들을 이용하여 다음과 같이 정의

      $ g(\mathbf x) = \sum_{i=1}^N g^{\mathcal R_i}(\mathbf x) \mathbf 1_{\mathcal R_i}(\mathbf x) $


  • 특성공간의 분할과 결정트리의 구성 : 특성공간 $\mathcal X$의 부분집합 $\mathcal A$와 (특성벡터에 대한) 어떤 분할규칙 $s$가 주어질 때, 집합 $\mathcal A$는 $s$가 참이 되게 하는 특성벡터들의 집합 $\mathcal A_{T}$와 거짓이 되게 하는 특성벡터들의 집합 $\mathcal A_{F}$로 분할할 수 있다. 즉, $\mathcal A = \mathcal A_{T}\cup \mathcal A_{F}$이고 $\mathcal A_{T}\cap \mathcal A_{F}=\varnothing$

    • 특성공간 $\mathcal X$와 분할규칙 $s$로부터 $\mathcal X = \mathcal X_{T}\cup \mathcal X_{F}$와 같은 분할을 얻는 것은 루트노드로부터 두 개의 자식노드를 얻는 것으로 이해할 수 있음

    • 따라서, 특성공간 $\mathcal X$를 두 개의 부분집합으로 분할하고, 각각의 부분집합을 다시 두 개의 부분집합으로 분할하는 계층적 분할 과정을 반복하면 대응되는 결정트리(이 경우에는 이진트리)를 얻을 수 있음

      • 루트노드에 대해 $N$ 세대 자식노드까지 구성할 때, 깊이(depth)가 $N$인 결정트리라고 함

    • 여러 가지 분할규칙을 사용할 수 있지만, 효율성을 고려하여 특성벡터 $\mathbf x=(x_1,x_2,\cdots,x_n)$의 한 특성 $x_i$를 기준값과 비교하는 분할규칙 $s_{i}^{\xi}$를 주로 사용

    $ s_i^{\xi}(\mathbf x)=s_i^{\xi}((x_1,x_2,\cdots,x_n))=\begin{cases} \text{True} & \ \text{if }x_i\le \xi\ \text{False} & \ \text{if } x_i > \xi\end{cases} $


  • 결정트리의 학습 알고리즘

  • 지금까지 살펴본 기계학습 모델과 달리 미리 정해진 모델 파라미터가 없음(실제로는 모든 훈련 데이터셋의 샘플이 파라미터 역할을 함)

    • 이런 모델을 비파라미터 모델(nonparametric model)이라고 함
    • 비파라미터 모델의 경우에는 과대적합이 될 가능성이 높으므로 자유도를 제한하는 다른 하이퍼파라미터를 사용

  • 문제에 맞는 손실함수 $\text{Loss}$를 정의하고, 앞에서 설명한 예측함수 $g$의 훈련 데이터셋에 대한 손실값 $ \ell(g)=\dfrac 1 m \sum_{i=1}^m \text{Loss}\bigl(y_i, g(\mathbf x_i)\bigr) $ 이 작아지도록 특성공간을 반복하여 분할해가는 과정이 학습 알고리즘.

    • 회귀문제의 경우 $\text{Loss}$ 함수 예: $\text{Loss}(y_i,g(\mathbf x_i))=(y_i-g(\mathbf x_i))^2$

      이 경우 훈련 데이터셋에 대한 손실값 $\ell(g)$는 MSE가 됨

    • 분류문제의 경우 $\text{Loss}$ 함수 예: $\text{Loss}(y_i,g(\mathbf x_i))=1-\mathbf 1_{{y_i}}\bigl(g(\mathbf x_i)\bigr)$

      이 경우 훈련 데이터셋에 대한 손실값 $\ell(g)$는 오분류율이 됨

  • 일반적으로 $\mathcal X$의 부분집합 $\mathcal A$를 분할규칙 $s$를 이용하여 $\mathcal A=\mathcal A_{T}\cup \mathcal A_{F}$로 분할할 때, 다음이 성립

    \[\begin{aligned} &\dfrac 1 m \sum_{i=1}^m \mathbf 1_{\mathcal A}(\mathbf x_i)\text{Loss}\bigl(y_i, g^{\mathcal A}(\mathbf x_i)\bigr)\\ \ge&\dfrac 1 m \sum_{i=1}^m \mathbf 1_{\mathcal A_{T}}(\mathbf x_i)\text{Loss}\bigl(y_i, g^{\mathcal A_{T}}(\mathbf x_i)\bigr) +\dfrac 1 m \sum_{i=1}^m \mathbf 1_{\mathcal A_{F}}(\mathbf x_i)\text{Loss}\bigl(y_i, g^{\mathcal A_{F}}(\mathbf x_i)\bigr) \end{aligned}\]

  • 따라서, 특성공간 $\mathcal X$로부터 시작하여 다음과 같이 현재 분할을 이루는 각각의 영역 $\mathcal A$에 대해 다음과 같이 귀납적으로 분할여부를 결정(CART 알고리즘: Classification and Regression Tree)

    • 고려하는 영역이 $\mathcal A$라 할 때,

      훈련 데이터셋의 각 특성벡터 $\mathbf x_i\ (1\le i \le m)$의 특성 $x_{ij}\ (1\le j\le n)$에 대한 분할규칙 $s_{j}^{x_{ij}}$에 따라 $\mathcal A$의 분할 $\mathcal A_T$, $\mathcal A_F$를 구하고, 다음 손실값

      \[\dfrac 1 m \sum_{i=1}^m \mathbf 1_{\mathcal A_{T}}(\mathbf x_i)\text{Loss}\bigl(y_i, g^{\mathcal A_{T}}(\mathbf x_i)\bigr) +\dfrac 1 m \sum_{i=1}^m \mathbf 1_{\mathcal A_{F}}(\mathbf x_i)\text{Loss}\bigl(y_i, g^{\mathcal A_{F}}(\mathbf x_i)\bigr)\]

      이 최소가 되는 $s_{j}^{x_{ij}}$를 이용하여 분할

    • 분할을 계속하면 손실값은 계속 작아지지만, 훈련 데이터셋에 과대적합되어 일반화 성능은 떨어질 수 있음

    • 또한, 매 단계에서 현 상황에서 최적의 분할을 선택하는 방법이므로, 몇 단계를 거쳐 손실값이 최소가 되는 경우는 고려하지 않는 방법임 (이런 의미로 CART 알고리즘을 탐욕적 알고리즘(greedy algorithm)이라고 함)

    • 과대적합을 방지하기 위해 $\mathcal A$에 대한 손실값과 $s_{j}^{x_{ij}}$를 이용하여 얻은 분할에 대한 손실값이 큰 차이가 없거나, 미리 정해둔 기준에 따라 분할을 더 이상 진행하지 않고 종료할 수 있음. 자유도를 규제하는 예는 다음과 같으며 설정하는 방법은 (그리드 탐색을 이용한) 교차검증을 통해 적절한 하이퍼파라미터를 결정

    • 자유도를 규제하는 것과 관계있는 사이킷런 결정트리 모델의 하이퍼파라미터들

      • 결정트리의 최대깊이 (max_depth)
      • 분할되기 위해 노드가 가져야 하는 최소 훈련 샘플의 개수 (min_samples_split)
      • 리프노드가 가지고 있어야 할 최소 훈련 샘플의 개수 (min_samples_leaf)
      • 리프노드의 최대 개수 (max_leaf_nodes)
      • 각 노드에서 분할에 사용할 특성의 최대 수 (max_features)
      • 분할을 통해 계산되는 불순도가 이 값보다 작을 때만 분할을 진행하게 하는 값 (min_impurity_decrease) : 이렇게 결정트리를 생성하는 것을 사전 가지치기(pre-pruning)

    • 과대적합을 조절하는 또 다른 방법으로 깊이가 최대인 결정트리를 생성한 후, 결정트리의 일부를 없애는 사후가지치기(post-pruning)를 적용할 수도 있음

  • 결정트리 분류기에서 사용하는 손실함수는 각 분할영역에 대한 불순도의 가중치 합으로 이해할 수 있음

  • 학습된 결정트리의 리프노드에 대응하는 $\mathcal X$의 분할이 $\mathcal X=\mathcal R_1\cup \cdots \cup \mathcal R_N$이라 할 때, 훈련 데이터셋에 대한 손실값은

    \[\begin{aligned} \ell(g)=&\dfrac 1 m \sum_{i=1}^m \text{Loss}\bigl(y_i,g(\mathbf x_i)\bigr)\\ =&\sum_{j=1}^N \dfrac 1 m \sum_{\mathbf x_i\in \mathcal R_j} \text{Loss}\bigl(y_i,g^{\mathcal R_j}(\mathbf x_i)\bigr)\\ =&\sum_{j=1}^N \dfrac {n_j} m \left(\dfrac 1 {n_j}\sum_{\mathbf x_i\in \mathcal R_j} \text{Loss}\bigl(y_i,g^{\mathcal R_j}(\mathbf x_i)\bigr)\right) \ (\text{단, $n_j$는 $R_j$에 속하는 샘플 수}) =&\sum_{j=1}^N \dfrac {n_j} m\, \text{IP}(\mathcal R_j) \end{aligned}\]

이고, 위 식에서 정의된 $\text{IP}(\mathcal R_j)$를 영역 $\mathcal R_j$에 대한 불순도(impurity)라고 함

  • 즉, 분류문제에서 결정트리의 훈련 데이터셋에 대한 손실값은 각 분할영역에 대한 불순도의 가중치합으로 이해할 수 있으므로 손실함수 대신 영역에 대한 불순도를 정의하면 학습을 시킬 수 있음
  • 학습에 사용할 수 있는 불순도의 예: 분류문제에 대한 결정트리에서, 분할영역 $\mathcal R^j$에 대해 $p_k$를 이 영역에 속하는 샘플 중 레이블이 $k$인 샘플의 비율, 즉
\[p_k = \dfrac{\sum_{i=1}^m \mathbf 1_{\{k\}}(y_i)}{\sum_{i=1}^m \mathbf 1_{\mathcal R_j}(\mathbf x_i)}, \ (1\le k\le K)\]

라 할 때,

  • 손실함수가 $\text{Loss}(y_i,g(\mathbf x_i))=1-\mathbf 1_{{y_i}}\bigl(g(\mathbf x_i)\bigr)$인 경우, 불순도 $\text{IP}(\mathcal R_j)$를 $\mathcal R_j$에 대한 오분류 불순도(misclassification impurity)라고 함

    • $g^ \{\mathcal R_j \}$는 $\max \{ p_k |1\le k\le K \} $를 함숫값으로 갖는 상수함수이므로 오분류 불순도는 $1-\max \{p_k | 1\le k\le K \}$

  • 엔트로피 불순도(Entropy Impurity)

    $ \text{IP}(\mathcal R_j)=-\sum_{k=1}^K p_k \log_2(p_k) $

  • 지니 불순도(Gini Impurity)

$ \text{IP}(\mathcal R_j)=1-\sum_{k=1}^K p_k^2 $

  • 지니 불순도가 조금 더 계산이 빠르므로 기본적인 불순도로 사용

  • 엔트로피 불순도는 좀 더 균형 잡힌 결정트리를 만드는 경향이 있음

  • 결정트리의 계산 복잡도

    • 결정트리를 이용하여 예측을 할 때, 루트노드부터 리프노드까지 탐색해야 하고 일반적으로 결정트리가 균형을 이루고 있으므로 대략 $O\bigl(\log_2(m)\bigr)$개 보다 작은 노드를 거치게 되므로 훈련 데이터셋의 크기가 아주 큰 경우에도 예측 속도가 아주 빠름
    • 결정트리의 각 리프노드에 대응되는 분할영역의 개수가 훈련 샘플의 개수 $m$과 같을 때 복잡도가 가장 큼
    • 트리가 균형을 이루고 있다고 가정하면 리프노드의 개수가 $m$일 때, 결정트리의 깊이는 대략 $\log_2(m)$

    • 훈련 알고리즘의 경우 복잡도가 가장 큰 경우는 모든 훈련 샘플의 모든 특성에 대해 비교를 해야 하므로 $O(n\times m\log_2 m)$이 됨

      • 훈련 데이터셋의 크기가 작을 때(수천 개 이하)는 미리 데이터를 정렬하여 훈련 속도를 높일 수 있지만, 훈련 데이터셋이 클 경우 속도가 많이 느려짐
      • 퀵 정렬의 복잡도 $O(m\log_2m)$


Reference:

  • 기계학습_하길찬 교수님 수업을 학습한 내용입니다.
← Previous Post Next Post →